前回の宿題
前々回の宿題に毛を生やす。
- "merged .sca file from HKL2000"を読み込んで異常分散差を表示する。
- 異常分散差の平均値を分解能シェルごとに表示する
処理の対象となるファイル情報(前回と同じ)
4行目以降の各行(1行に書いてある)には以下の情報が含まれている H,K,L,I(+),sigI(+),I(-),sigI(-) ただし、(-)が無い場合には情報は「ファイルに書き出されていない」。 I(+)が無い場合、I(+)=0, sigI(+)=-1が入るみたい。
プログラム仕様
- コマンドラインからファイル名を指定
- ファイルを開いて行を読み込んでいく
- 3行目にある格子定数を文字列でも何でもよいから取り込んで後で表示でき るようにしておく
- 4行目以降では読み込んだカラム数が5の場合、異常分散差は計算できない
ので無視、カラム数が7の場合、以下の式を計算していく。
bunshi=|I(+)-I(-)| bunbo=(sigI(+)+sigI(-))/2.0 delano=bunshi/bunbo (ただし、分母が0の場合は無視) (式については別の機会に議論)
- delanoを反射ファイルが続く限り分解能シェルごとに足し続け、平均します
宿題の答えと解説
暫定版回答 081120
インラインにて軽く説明
#!/usr/bin/env python #$ -S /usr/bin/python import sys import math ############################################################# # calc_rcell function: (1)関数を定義してみた ############################################################# def calc_rcell(cell_string): # obtaining each cell parameter cell=cell_string.split() # Delete the last columns del cell[6:] # (2)配列を削除してみた # deg->rad d2r=math.pi/180.0 # Preparation a=float(cell[0]) #(3)型を変換してみた b=float(cell[1]) c=float(cell[2]) alph=float(cell[3]) beta=float(cell[4]) gamm=float(cell[5]) # Calculation simple coeficients sin_a=math.sin(alph*d2r) # (4)三角関数を使ってみた sin_b=math.sin(beta*d2r) sin_g=math.sin(gamm*d2r) cos_a=math.cos(alph*d2r) cos_b=math.cos(beta*d2r) cos_g=math.cos(gamm*d2r) # Calculation of cos^2(alph) cos_a2=math.pow(cos_a,2.0) cos_b2=math.pow(cos_b,2.0) cos_g2=math.pow(cos_g,2.0) abc=a*b*c # Calculation of cell volume v=abc*math.sqrt(1.0-cos_a2-cos_b2-cos_g2+2.0*cos_a*cos_b*cos_g) # Reciprocal vectors cos_as=(cos_b*cos_g-cos_a)/(sin_b*sin_g) cos_bs=(cos_g*cos_a-cos_b)/(sin_g*sin_a) cos_gs=(cos_a*cos_b-cos_g)/(sin_a*sin_b) as=b*c*sin_a/v bs=c*a*sin_b/v cs=a*b*sin_g/v # return reciprocal cell parameters rcell=[as,bs,cs,math.acos(cos_as),math.acos(cos_bs),math.acos(cos_gs)] return rcell #(5)関数からの戻り値を設定してみた ############################################################# # calculating resolution ############################################################# def calc_resol(h,k,l,rcell): # preparation h2=h*h k2=k*k l2=l*l # reciprocal cell parameters as=rcell[0] bs=rcell[1] cs=rcell[2] as2=as*as bs2=bs*bs cs2=cs*cs cos_as=math.cos(rcell[3]) cos_bs=math.cos(rcell[4]) cos_gs=math.cos(rcell[5]) # calculating d* ds2=h2*as2+k2*bs2+l2*cs2+2.0*(k*l*bs*cs*cos_as+l*h*cs*as*cos_bs+h*k*as*bs*cos_gs) ds=math.sqrt(ds2) # storing resolution resol=1.0/ds return resol ############################################################# # shell division ############################################################# def which_shell(resmin,resmax,resol,nshell=10): #(6)関数の引数に初期値を入れてみた # calculating (dmin^3),(dmax^3),(d^3) d3min=math.pow(1/resmin,3.0) d3max=math.pow(1/resmax,3.0) d3cur=math.pow(1/resol,3.0) # shell selection dwidth=(d3max-d3min)/nshell for i in range(0,10): tmp_min=d3min+i*dwidth tmp_max=d3min+(i+1)*dwidth if d3cur<tmp_max and d3cur>=tmp_min: return i return -1 ############################################################# # calculating median ############################################################# def getMedian(resmin,resmax,nshell,idx): # calculating (dmin^3),(dmax^3),(d^3) d3min=math.pow(1/resmin,3.0) d3max=math.pow(1/resmax,3.0) # shell selection dwidth=(d3max-d3min)/nshell tmp_min=d3min+idx*dwidth tmp_max=d3min+(idx+1)*dwidth tmp_mean=(tmp_min+tmp_max)/2.0 target=1.0/math.pow(tmp_mean,1/3.0) return target ############################################################# # Main function ############################################################# if len(sys.argv)!=4: print "Usage: readAnoSca SCAFILE MINRES MAXRES" sys.exit() else: print "Processing %s"%sys.argv[1] # (7)printしてみた # File open infile=open(sys.argv[1],'r') # Minimum & Maximum resolution minres=float(sys.argv[2]) maxres=float(sys.argv[3]) if minres < maxres: print "MINRES should be a larger value than MAXRES" sys.exit(0) # reading all of lines linelist=infile.readlines() # initialization of parameters nline=0 # line counter nok=0 # number of reflections with anomalous nshell=10 sumSN=[0]*nshell #(8)変数の配列を初期化してみた cntSN=[0]*nshell # acquiring cell parameters at the 3rd line cell_string=linelist[2] rcell=calc_rcell(cell_string) # (9)関数を使ってみた # treating each line for line in linelist: # counting a number of line nline+=1 # initialization strings=line.split() # counting a number of columns ncolumn=len(strings) # data processing # ncolumn=7: anomalous signals can be obtained # ncolumn=5: anomalous signals cannot be obtained if ncolumn==7 and nline>4: # acquiring HKL indices h=int(strings[0]) k=int(strings[1]) l=int(strings[2]) # calculating resolution resol=calc_resol(h,k,l,rcell) if resol < minres and resol > maxres: # 分解能選択 # choosing which shell idx=which_shell(minres,maxres,resol,nshell) if idx==-1: print "Critical error!\n" continue else: continue # for I(+)s i_plus=float(strings[3]) sig_plus=float(strings[4]) # case when I(+) was not observed -> skip this reflection if i_plus==0 and sig_plus==-1.0: continue # for I(-)s i_minus=float(strings[5]) sig_minus=float(strings[6]) # difference between I(+) and I(-) nok+=1 bunshi=math.fabs(i_plus-i_minus) bunbo=(sig_plus+sig_minus)/2.0 snvalue=bunshi/bunbo if snvalue>0.0: sumSN[idx]+=snvalue cntSN[idx]+=1 # Final calculation of average :全てのシェルに対して計算結果を表示する for i in range(0,nshell): median=getMedian(minres,maxres,nshell,i) dstar2=1.0/median/median print "%5.2f %5.3f %5d %8.2f" % (median,dstar2,cntSN[i],sumSN[i]/cntSN[i])
つこてるテク
(1)関数を定義してみた
プログラム言語ではよく使う機能を持つ処理の塊を「関数」として定義して1行で呼び出すことをよくする。Pythonでもこれまで勉強してきたように標準で入っている関数を使ってプログラムを簡単に書いてきた。無意識のうちに関数と言う概念を利用してプログラムを書いているのだ。
infile=open(filename,'r')
↑関数の利用例。1行で「名前がfilenameのファイルを見つけ、メモリ空間に読み込んできて先頭アドレスをinfileに格納する」という仕事をやってのけている。というような関数を自分でも定義できる。定義のしかたは
def foo(hee1,hee2,....):
って感じ。ここでfooは関数の名前。hee1, hee2は引数(パラメータ)と呼ぶ。関数の設計は呼ぶ側と呼ばれる側をよく考えて行なう必要がある。
引数によって呼び出す側から呼び出される側へ変数が渡される。
def print_hey(comment):
print comment
def main:
print_hey("konoyaro")
このプログラムの実行結果は "konoyaro"が画面上に表示される。この場合だとmain関数からprint_key関数を呼び出している。
print_key関数を呼び出す時に、main側では"konoyaro"という文字列をprint_key関数に渡している。この後、print_key関数はこの引数を画面に表示する、という作業を行なうが、それはまるっきりmainから渡された変数を利用している。
ここで覚えておきたいことは以下2点。
- 関数という機能の塊を定義することが出来る
- 関数にはパラメータを渡すことが出来る
(2)配列を削除してみた
不要な配列を削除する。配列オブジェクトに対して実行できる関数のようですが、
del foo[3:5] # 配列の要素3〜要素5まで削除 del foo[3:] # 配列の要素3〜後を削除 del foo[:3] # 配列の要素3までを削除
てな感じらしい。ここでは要素が7個の配列があって、先頭から6個までが必要なので7個目以降を削除するという命令として
del foo[6:]
を使用している。
(3)型変換をやってみた
Pythonはプログラム言語の中では珍しく変数の型を宣言して利用することがほとんどない。そのため、気をつけてコーディングしていかないと、今扱っている変数が何者か分からなくなってしまう。ここでは文字列配列からゲットしてきた格子定数を文字列ではなく数値として以降利用できるようにあえて明示的に型変換している。
a=float(cell[0])
この作業によって、cell[0]の文字列はfloat型(浮動小数)に変換されて変数aに代入される。
(4)三角関数を使ってみた
三角関数など数学的な数式はmathモジュールをインポートして用いることが可能。わけの分からない言い方をしているが、なれるまで言いまくってなれてしまいましょう。mathモジュールをインポートするには
import math
とする必要がある。これによって数学的処理に必要な関数がバコバコ使えるようになる。
sin_a=math.sin(alph*d2r) # math.sin() sin関数 zettaichi=math.fabs(value) # math.fabs():絶対値関数 root_2=math.sqrt(2) # math.sqrt():平方根関数
(5)関数からの戻り値を設定してみた
関数は前述のように呼び出し側と呼び出される側の関係をよく洗い出して設計をした方が後々楽。calc_rcell関数をみて欲しい。main側ではcell_stringという.scaファイルの格子定数を含んだ行を文字列として取り込んでcalc_rcell関数に渡している。calc_rcell関数はその名の通り、逆格子を計算しているが、最後に配列rcellをreturnしている。
return(rcell)
関数がmain側から何らかの処理を依頼されて、最終的にreturnでmain側へ変数を返す時、返る値のことを戻り値/返り値などと言う。
(6)printしてみた
print関数は何気に分かりにくい。
print x
とすれば変数Xがまんまプリントされる。この場合、xの型が勝手にprintで解釈されて表示されるので意図していない表示がされる場合が多々ある。
こんなとき、フォーマットしたprintが便利。
x=3 print "%5d" % x print "%8.4f" % x print "%s" % x
などというプログラムを実行すると実行結果は
3 3.0000 3
となるだろう。%の後の数字は桁数(.を含む)。数字の後のアルファベットは d:整数、f:浮動小数、s:文字列などの表示の際の型。浮動小数の場合の点の後の数値(上記では 8.4の4)は小数点以下の数字の桁数。を表している。ダブルクヲーテーションで囲んだ指定フォーマットに対して%で区切って変数を後ろに並べていく。複数変数がある場合は、
x=3, y=4 print "%8.3f %8.3f" % (x,y)
となる(はず)。
(8)変数の配列を初期化してみた
前述の通り、Pythonでは事前に明示的に変数を定義することは少ない。しかし、今回のように配列を指定した数確保しそれらを初期化する場合は、後から処理すると大変面倒だったり、わけが分からなくなってしまう。そこで事前に変数定義をしている。
sumSN=[0]*nshell
これでnshell個の配列を0で初期化してsumSNに入れておいてね、という定義になる。最初私は
sumSN=[10]
などとしていたが、これだと10という値の配列1個の定義になる。無念。
(9)関数を使ってみた
定義した関数は使ってみるべし。関数定義のありがたみと設計の重要さがわかってくる。それまでは関数を作りまくって慣れてしまおう。
rcell=calc_rcell(cell_string)
calc_rcell関数は最終的に逆格子パラメータの配列(要素数6)を返してくるのでこれをrcellという変数で受けている。受けた瞬間、rcellは要素数6の配列に型を変形する。
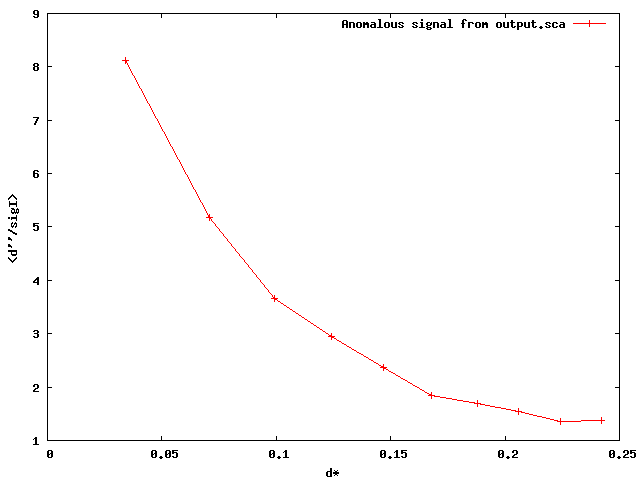
使用例
出力情報とGNUPLOTを使えば、こんなプロットが出来るよ